martes, 11 de febrero de 2014

FORMULA GENERAL DE LAS ECUACIONES CUADRATICAS

¿Qué tienen de especial?

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:

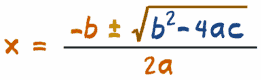
	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!

	La parte azul (b² - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios .

Solución

Para resolverla, sólo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos.

Ejemplo: resuelve 5x² + 6x + 1 = 0

Fórmula cuadrática: x = [ -b ± √(b²-4ac) ] / 2a

Los coeficientes son: a = 5, b = 6, c = 1

Sustituye a,b,c: x = [ -6 ± √(6²-4×5×1) ] / 2×5

Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10

Respuesta: x = -0.2 and -1

(Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)

Ecuaciones cuadráticas disfrazadas

Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:

Disfrazadas	Qué hacer	En forma estándar	a, b y c
x² = 3x -1	Mueve todos los términos a la izquierda	x² - 3x + 1 = 0	a=1, b=-3, c=1
2(x² - 2x) = 5	Desarrolla paréntesis	2x² - 4x - 5 = 0	a=2, b=-4, c=-5
x(x-1) = 3	Desarrolla paréntesis	x² - x - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x² = 0	Multiplica por x²	5x² + x - 1 = 0	a=5, b=1, c=-1

MAPA MENTAL

VIDEOS

http://es.slideshare.net/adriachan/frmula-general

PRESENTACION

http://es.slideshare.net/adriachan/frmula-general

conclucion

La fórmula general es un procedimiento que se usa para factorizar polinomios de la forma ax^2+bx+c, con a,b y c constantes reales y a diferente a cero.

TEOREMA DE PITAGORAS

Teorema de Pitágoras

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:

Si el triángulo tiene un ángulo recto (90°)...

... y pones un cuadrado sobre cada uno de sus lados, entonces...

... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²):

a² + b² = c²

¿Seguro... ?

Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.

Veamos si las áreas son la misma:

3² + 4² = 5²

Calculando obtenemos:

9 + 16 = 25

¡sí, funciona!

¿Por qué es útil esto?

Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)

¿Cómo lo uso?

Escríbelo como una ecuación:

a² + b² = c²

Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:

a² + b² = c²

5² + 12² = c²

25 + 144 = 169

c² = 169

c = √169

c = 13

a² + b² = c²

9² + b² = 15²

81 + b² = 225

Resta 81 a ambos lados

b² = 144

b = √144

b = 12

MAPA MENTAL

VIDEOS

http://www.youtube.com/watch?v=Pm_ncQVCWlA

PRESENTACION

http://es.slideshare.net/johancaballero/teorema-de-pitagoras-1078512

CONCLUCION

sabiendo dos de los tres elementos que te solicita el teorema podes obtener el otro... que existe una igualdad entre el cuadrado de la hipotenusa y la suma del cuadrado de los catetos.. y que es aplicable a los triangulos rectángulos...

HOMOTECIA INVERSA Y DIRECTA

HOMOTECIAS

Las homotecias transforman una figura plana en otra figura de igual forma, pero de menor o mayor tamaño, según el valor de la razón, k. Si kes positivo la homotecia es directa, y si no, es inversa.

- Homotecias
Una homotecia de centro O y razón de semejanza k (k > 0) es la transformación que hace corresponder a cada punto P otro punto P′, alineado con O y P, de forma que ...

- Homotecia directa y homotecia inversa
En una homotecia de centro el punto O y razón k:. Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa. Si k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa. . A la figura ABCD le hemos aplicado...

- Propiedades de las homotecias

1.o Toda recta que pasa por el centro de homotecia es invariante, es decir, se transforma en sí misma. . . 2.o Toda recta que no pasa por el centro de homotecia se transforma en otra recta paralela a la dada. 3.o La razón de dos segmentos homotéticos es...

Homotecia directa y homotecia inversa

En una homotecia de centro el punto O y razón k:

Si k > 0, A y A′ están al mismo lado de O, y se dice que lahomotecia es directa.
Si k < 0, A y A′ están a distinto lado de O, y se dice que lahomotecia es inversa.

A la figura ABCD le hemos aplicado una homotecia de centro O y razónk, con k > 0; homotecia directa.
A la figura ABC le hemos aplicado una homotecia de centro O y razón k, con k < 0; homotecia inversa.

HOMOTECIA DIRECTA

HOMOTECIA INVERSA

Propiedades de las homotecias

1.^o Toda recta que pasa por el centro de homotecia es invariante, es decir, se transforma en sí misma.

HOMOTECIA RECTA

------------------------------------------------------------------------------------------------------------------------------------

2.^o Toda recta que no pasa por el centro de homotecia se transforma en otra recta paralela a la dada.
3.^o La razón de dos segmentos homotéticos es igual a la razón k de la homotecia.

SEGMENTOS HOMOTETICOS

--------------------------------------------------------------------------------------------------------------

4.^o Una homotecia transforma los ángulos en ángulos iguales.

Tipos de homotecia:
1.-HOMOTECIA DIRECTA: es aquella en la cual el punto de homotecia o el centro de homotecia se encuantra despues o antes de la figura trazada. La caracteriztica principal es que los segmentos entre las figuras son paralelas.

2.-HOMOTECIA INVERSA: Es aquella en la cual el centro de homotecia se encuentra entre la figura.

La homotecia tambien puede ser positiva o negativa. Determinan la razon que se tome es decir, el factor principal por el cual se multiplica.
Para encontrar la razon de homotecia debe colocarse uno a uno cada lado o segmento de las figuras y sacar la constante de proporcionalidad.

MAPA MENTAL

VIVIDEOS

http://www.youtube.com/watch?v=T2AdPgCykVE

http://www.youtube.com/watch?v=DiftHbfjM6M

PRESENTACION

media.wix.com/.../ad327d_c5a13dcab61aadb2beaecbd217681487.ppt?.

www.geocities.ws/gd_lam02/11_02_HEXAEDRO.pps‎

CONCLUCION

La homotecia es otra forma de obtener figuras a escala. Bastará con multiplicar la medida del centro de homotecia al punto seleccionado de la figura real por la escala propuesta; el resultado, es la distancia que deberá medirse del centro al punto homotético correspondiente.

SIMETRIA AXIAL Y CENTRAL

SIMETRÍA AXIAL

La simetría axial (también llamada rotacional, radial o cilíndrica) es lasimetría alrededor de un eje, de modo que un sistema tiene simetría axial oaxisimetría cuando todos los semiplanos tomados a partir de cierto eje y conteniéndolo presentan idénticas características.

La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.

SIMETRÍA AXIAL DE UN TRIANGULO

A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. En este caso: La simetría axial se puede dar también en un objeto con respecto de uno o más ejes de simetría.

Si se doblara la figura sobre el eje de simetría trazado, se podría observar con toda claridad que los puntos de las partes opuestas coinciden, es decir, ambas partes son congruentes.

SIMETRÍA CENTRAL

La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto llamado imagen, que debe cumplir las siguientes condiciones:

a) El punto y su imagen están a igual distancia de un punto llamado centro de simetría.

b) El punto, su imagen y el centro de simetría pertenecen a una misma recta.

SIMETRÍA CENTRAL DEL PUNTO A

SIMETRÍA CENTRAL DEL TRIANGULO ABC, RESPECTO DEL PUNTO 0

MAPA MENTAL

VIDEOS

http://www.youtube.com/watch?v=q8ZcOkh7030

PRESENTACION

http://es.slideshare.net/miriamvega12/simetria-axial-9037991

matematicasmerlin.wikispaces.com/file/view/Clase%20simetria.ppt‎

CONCLUCION

La simetría axial es la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando al cortar dicho sistema por un semiplano que contiene al eje el resultado es siempre el mismo.

Se suele decir que una figura tiene simetría central o simetría radial cuando se puede hacer coincidir consigo misma mediante varios giros. Sin embargo, la expresión no es matemáticamente correcta

TRASLACION DE FIGURAS

TRASLACIÓN

Otro tipo de transformaciones isométrica de una figura en el plano es la traslación, producida al desplazarse dicha figura a través de paralelas en una dirección dada. La figura mantiene su forma y tamaño.

Para trasladar una figura debemos de considerar lo siguiente :

a) trazar una recta por uno de los vértices de la figura en la dirección deseada.

b) posteriormente se trazan paralelas a la recta dibujada anteriormente, por

cada uno de los vértices de la figura,

c) se elige una distancia d cualquiera para trasladar la figura. Esa misma

distancia se aplica en cada una de las paralelas dibujadas. Uniendo los puntos

obtenidos se obtiene la imagen de la figura dada.

MAPA MENTAL

VIDEOS

http://www.youtube.com/watch?v=YvJiZsgZbAY

http://www.youtube.com/watch?v=ENglZuRlozk

PRESENTACION

ww2.educarchile.cl/PORTAL.HERRAMIENTAS/.../1262006174733.ppt‎

CONCLUCION

Aunque para trasladar una figura hay que trasladar todos sus puntos, a veces basta con trasladar algunos puntos particulares para obtener la figura trasladada.

Por ejemplo, para trasladar un polígono, basta con trasladar sus vértices, como puedes ver en la figura adjunta.

Si varías el vector guía recuerda que cualquier segmento y cualquier ángulo han de valer lo mismo que su trasladado. Además los ángulos conservan también la orientación.

Movimientos en el plano :)

ROTACION DE FIGURAS

una rotación es una transformación al plan o al espacio que describe el movimiento de un sólido rígido alrededor de un eje. En una rotación pura los puntos del eje son fijas, dicho de otro modo, la posición de los punto del eje quedan en el mismo lugar un golpe transformados. Una rotación se diferencia de una traslación, la cual desplaza todos los puntos del sólido por igual y no mantiene puntos fijas, y de una reflexión, que tumban el sólido creando una imagen especular. Las tres transformaciones descritas dejen inalterades las distancias entre parejas de puntos; son isometrícas.

ara rotar una figura Se une un vértice de la figura con el centro de rotación mediante un segmento, se traza desde el segmento el ángulo indicado para la rotación y se mide la misma longitud que tiene el segmento anterior marcando el punto imagen.
Se hace lo mismo con cada vértice de la figura y se unen todos los puntos resultantes.
La figura que se obtiene es la imagen por rotación de la figura original.
El centro de rotación puede estar dentro o fuera de la figura.

MAPA MENTAL

VIDEOS

http://www.youtube.com/watch?v=ENglZuRlozk

http://www.youtube.com/watch?v=1YuG3hBe1hc

PRESENTACION

ww2.educarchile.cl/PORTAL.HERRAMIENTAS/.../1262006174733.ppt‎

CONCLUSION

las rotaciones son movimientos directos es decir que mantienen la forma y el tamaño que tienen las

figuras, cada punto se transforma en otro describiendo un arco de circunsferencia alrrededor del centro.

la distancia del punto dado al centro de la rotacion debe ser la misma que la del punto transformado y el centro

de rotacion.